問1
図のように,紙面に平行な平面内の平等電界E[V/m]中で2Cの点電荷を点Aから点Bまで移動させ,さらに点Bから点Cまで移動させた。この移動に,外力による仕事W=14Jを要した。点Aの電位に対する点の電位Vʙᴀ[V]の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,点電荷の移動はゆっくりであり,点電荷の移動によってこの平等電界は乱れないものとする。
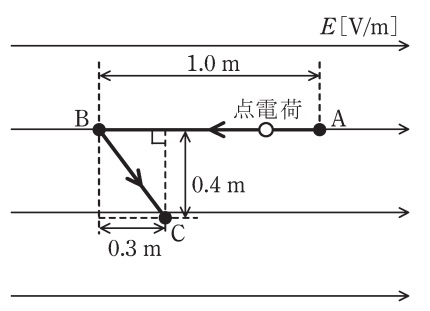
- 5
- 7
- 10
- 14
- 20
- 解答
問2
四本の十分に長い導体円柱①~④が互いに平行に保持されている。①~④は等しい直径を持ち,図の紙面を貫く方向に単位長さあたりの電気量+Q[C/m] 又は−Q[C/m]で均一に帯電している。ただし, Q>0とし,①の帯電電荷は正電荷とする。円柱の中心軸と垂直な面内の電気力線の様子を図に示す。ただし,電気力線の向きは示していない。このとき,①~④の帯びている単位長さあたりの電気量の組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
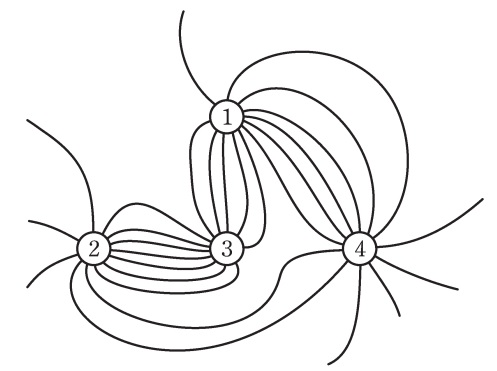
| ① | ② | ③ | ④ | |
|---|---|---|---|---|
| 1 | +Q | +Q | +Q | +Q |
| 2 | +Q | +Q | −Q | −Q |
| 3 | +Q | −Q | +Q | +Q |
| 4 | +Q | −Q | −Q | −Q |
| 5 | +Q | +Q | +Q | −Q |
- 解答
問3
平等な磁束密度B₀[T]のもとで,一辺の長さがh[m]の正方形ループABCDに直流電流I[A]が流れている。B₀の向きは辺ABと平行である。B₀がループに及ぼす電磁力として,正しいものを次の(1)~(5)のうちから一つ選べ。
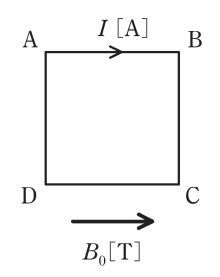
- 大きさ2IhB₀[N]の力
- 大きさ4IhB₀[N]の力
- 大きさIh²B₀[N⋅m]の偶力のモーメント
- 大きさ2Ih²B₀[N⋅m]の偶力のモーメント
- 力も偶力のモーメントも働かない
- 解答
問4
磁力線は,磁極の働きを理解するのに考えた仮想的な線である。この磁力線に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
- 磁力線は,磁石のN極から出てS極に入る。
- 磁極周囲の物質の透磁率をμ[H/m]とすると, m[Wb]の磁極からm/μ本の磁力線が出入りする。
- 磁力線の接線の向きは,その点の磁界の向きを表す。
- 磁力線の密度は,その点の磁束密度を表す。
- 磁力線同士は,互いに反発し合い,交わらない。
- 解答
問5
次に示す, A,B,C, Dの四種類の電線がある。いずれの電線もその長さは1kmである。この四つの電線の直流抵抗値をそれぞれ Rᴀ[Ω],Rʙ[Ω],Rc[Ω],Rᴅ[Ω]とする。Rᴀ~Rᴅの大きさを比較したとき,その大きさの大きい順として,正しいものを次の(1)~(5)のうちから一つ選べ。
ただし,ρは各導体の抵抗率とし,また,各電線は等断面,等質であるとする。
A:断面積が9×10⁻⁵m²の鉄( ρ=8.90×10⁻⁸ Ω⋅m )でできた電線
B:断面積が5×10⁻⁵m²のアルミニウム( ρ=2.50×10⁻⁸ Ω⋅m )でできた電線
C:断面積が1×10⁻⁵m²の銀( ρ=1.47×10⁻⁸ Ω⋅m )でできた電線
D:断面積が2×10⁻⁵m²の銅( ρ=1.55×10⁻⁸ Ω⋅m )でできた電線
- Rᴀ>Rᴄ>Rᴅ>Rʙ
- Rᴀ>Rᴅ>Rᴄ>Rʙ
- Rʙ>Rᴅ>Rᴄ>Rᴀ
- Rᴄ>Rᴀ>Rᴅ>Rʙ
- Rᴅ>Rᴄ>Rᴀ>Rʙ
- 解答
問6
図のように,三つの抵抗R₁=3Ω,R₂=6Ω,R₃=2Ωと電圧V[V]の直流電源からなる回路がある。抵抗R₁, R₂,R₃の消費電力をそれぞれP₁[W],P₂[W],P₃[W]とするとき,その大きさの大きい順として,正しいものを次の(1)~(5)のうちから一つ選べ。

- P₁>P₂>P₃
- P₁>P₃>P₂
- P₂>P₁>P₃
- P₂>P₃>P₁
- P₃>P₁>P₂
- 解答
問7
図のように,直流電源にスイッチS,抵抗5個を接続したブリッジ回路がある。この回路において,スイッチSを開いたとき,Sの両端間の電圧は1Vであった。スイッチSを閉じたときに8Ωの抵抗に流れる電流Iの値[A]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
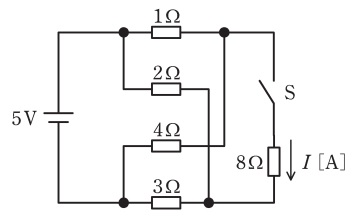
- 0.10
- 0.75
- 1.0
- 1.4
- 2.0
- 解答
問8
図のように,静電容量2μFのコンデンサ,R[Ω]の抵抗を直列に接続した。この回路に,正弦波交流電圧10V,周波数1000Hzを加えたところ,電流0.1Aが流れた。抵抗Rの値[Ω]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
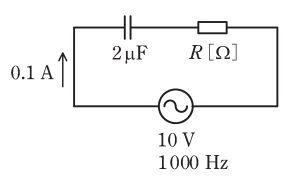
- 4.50
- 20.4
- 30.3
- 60.5
- 79.6
- 解答
問9
図のように,R[Ω]の抵抗,インダクタンスL[H]のコイル,静電容量C[F]のコンデンサと電圧[V],角周波数ω[rad/s]の交流電源からなる二つの回路AとBがある。両回路においてそれぞれω²LC=1が成り立つとき,各回路における図中の電圧ベクトルと電流ベクトルの位相の関係として,正しいものの組合せを次の(1)~(5)のうちから一つ選べ。ただし,ベクトル図における進み方向は反時計回りとする。
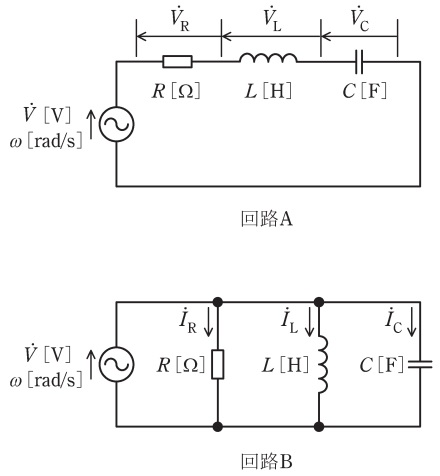
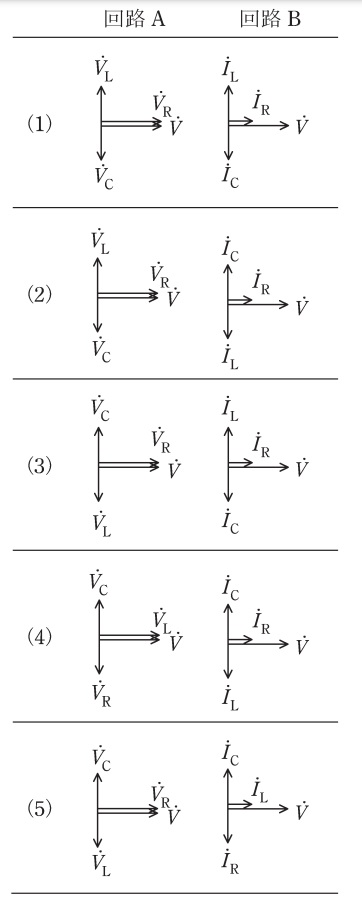
- 解答
問10
図の回路のスイッチを閉じたあとの電圧 v(t)の波形を考える。破線から左側にテブナンの定理を適用することで,回路の時定数[s]とv(t)の最終値[V]の組合せとして,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,初めスイッチは開いており,回路は定常状態にあったとする。
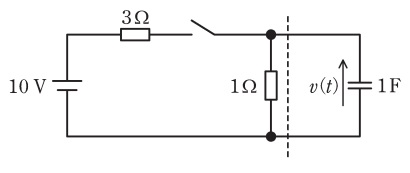
| 時定数[s] | 最終値[V] | |
|---|---|---|
| 1 | 0.75 | 10 |
| 2 | 0.75 | 2.5 |
| 3 | 4 | 2.5 |
| 4 | 1 | 10 |
| 5 | 1 | 0 |
- 解答
問11
次の文章は,可変容量ダイオード(バリキャップやバラクタダイオードともいう)に関する記述である。
可変容量ダイオードとは,図に示す原理図のように(ア)電圧V[V]を加えると静電容量が変化するダイオードである。p形半導体とn形半導体を接合すると,p形半導体のキャリヤ(図中の●印)とn形半導体のキャリヤ(図中の〇印)がpn接合面付近で拡散し,互いに結合すると消滅して(イ)と呼ばれるキャリヤがほとんど存在しない領域が生じる。可変容量ダイオードに(ア) 電圧を印加し,その大きさを大きくすると,(イ)の領域の幅 d が(ウ)なり,静電容量の値は(エ) なる。この特性を利用して可変容量ダイオードは(オ)などに用いられている。
上記の記述中の空白箇所(ア)~(オ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
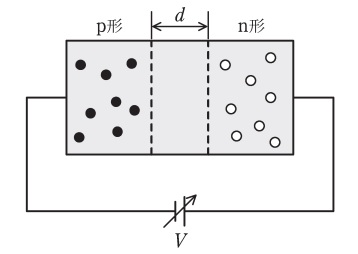
| ア | イ | ウ | エ | オ | |
|---|---|---|---|---|---|
| 1 | 逆方向 | 空乏層 | 広く | 小さく | 無線通信の同調回路 |
| 2 | 順方向 | 空乏層 | 狭く | 小さく | 光通信の受光回路 |
| 3 | 逆方向 | 空乏層 | 広く | 大きく | 光通信の受光回路 |
| 4 | 順方向 | 反転層 | 狭く | 大きく | 無線通信の変調回路 |
| 5 | 逆方向 | 反転層 | 広く | 小さく | 無線通信の同調回路 |
- 解答
問12
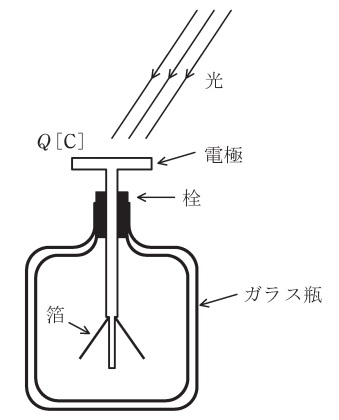
次のような実験を真空の中で行った。
まず,箔検電器の上部アルミニウム電極に電荷Q[C]を与えたところ,箔が開いた状態になった。次に,箔検電器の上部電極に赤外光,可視光,紫外光の順に光を照射したところ,紫外光を照射したときに箔が閉じた。
ただし,赤外光,可視光,紫外光の強度はいずれも上部電極の温度をほとんど上昇させない程度であった。
この実験から分かることとして,正しいものを次の(1)~(5)のうちから一つ選べ。
- 電荷Qは正電荷であった可能性も負電荷であった可能性もある。
- 紫外光が特定の強度よりも弱いとき箔はまったく閉じなくなる。
- 赤外光を照射したとき上部電極に熱電子が吸収された。
- 可視光を照射したとき上部電極の電気抵抗が大幅に低下した。
- 紫外光を照射したとき上部電極から光電子が放出された。
- 解答
問13
演算増幅器及びそれを用いた回路に関する記述として,誤っているものを次の(1)~(5)のうちから一つ選べ。
- 演算増幅器には電源が必要である。
- 演算増幅器の入力インピーダンスは,非常に大きい。
- 演算増幅器は比較器として用いられることがある。
- 図1の回路は正相増幅回路,図2の回路は逆相増幅回路である。
- 図1の回路は,抵抗Rꜱを0Ωに(短絡)し,抵抗Rꜰを∞Ωに(開放)すると,ボルテージホロワである。

- 解答
問14
物理現象と,その計測・検出のための代表的なセンサの原理との組合せとして,不適切なものを(1)~(5)のうちから一つ選べ。
| 物理現象 (計測・検出対象) |
センサの原理 | |
|---|---|---|
| 1 | 光 | 電磁誘導に関する ファラデーの法則 |
| 2 | 超音波 | 圧電現象 |
| 3 | 温度 | ゼーベック効果 |
| 4 | 圧力 | ピエゾ抵抗効果 |
| 5 | 磁気 | ホール効果 |
- 解答
問15
図のように,線間電圧(実効値)200Vの対称三相交流電源に,1台の単相電力計W₁,X=4Ωの誘導性リアクタンス3個,R=9Ωの抵抗3個を接続した回路がある。単相電力計W1の電流コイルはa相に接続し,電圧コイルはb-c相間に接続され,指示は正の値を示していた。この回路について,次の(a)及び(b)の問に答えよ。
ただし,対称三相交流電源の相順は,a,b,cとし,単相電力計W₁の損失は無視できるものとする。
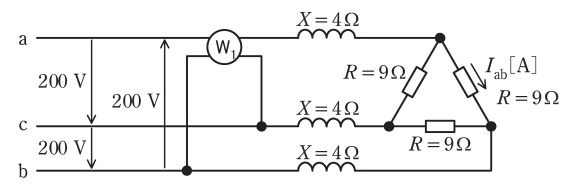
(a)R=9Ωの抵抗に流れる電流Ia𝚋の実効値 [A] として,最も近いものを次の(1)~(5)のうちから一つ選べ。
- 6.77
- 13.3
- 17.3
- 23.1
- 40.0
- 解答
(b)単相電力計W₁の指示値[kW]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0
- 2.77
- 3.70
- 4.80
- 6.40
- 解答
問16
最大目盛150V ,内部抵抗18kΩの直流電流計V₁と最大目盛300V,内部抵抗30kΩの直流電圧計V₂の二つの直流電圧計がある。ただし,二つの直流電圧計は直動式指示電気計器を使用し,固有誤差はないものとする。次の(a)及び(b)の問に答えよ。
(a)二つの直流電圧計を直列に接続して使用したとき,測定できる電圧の最大の値[V]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
- 150
- 225
- 300
- 400
- 450
- 解答
(b)次に,直流電圧450Vの電圧を測定するために,二つの直流電圧計の指示を最大目盛にして測定したい。そのためには,直流電圧計(ア)に,抵抗(イ)kΩを(ウ)に接続し,これに直流電圧計(エ)を直列に接続する。このように接続して測定することで,各直流電圧計の指示を最大目盛にして測定をすることができる。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。
| ア | イ | ウ | エ | |
|---|---|---|---|---|
| 1 | V₁ | 90 | 直列 | V₂ |
| 2 | V₁ | 90 | 並列 | V₂ |
| 3 | V₂ | 90 | 並列 | V₁ |
| 4 | V₁ | 18 | 並列 | V₂ |
| 5 | V₂ | 18 | 直列 | V₁ |
- 解答
問17
図のように,誘電体の種類,比誘電率,絶縁破壊電界,厚さがそれぞれ異なる三つの平行板コンデンサ①~③がある。極板の形状と大きさは同一で,コンデンサの端効果,初期電荷及び漏れ電流は無視できるものとする。上側の極板に電圧V₀[V]の直流電源を接続し,下側の極板を接地した。次の(a)及び(b)の問に答えよ。
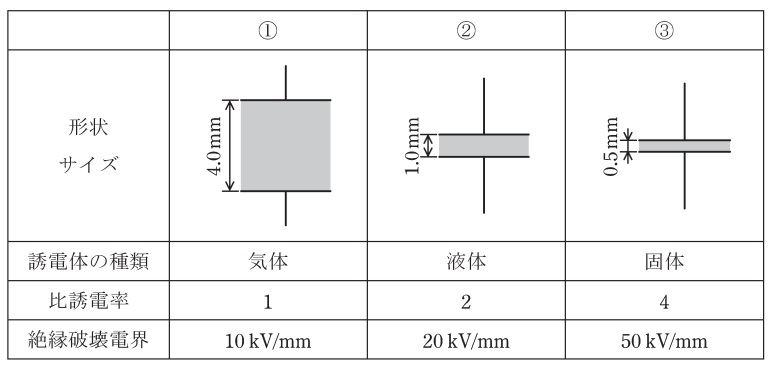
(a)各平行板コンデンサへの印加電圧の大きさが同一のとき,極板間の電界の強さの大きい順として,正しいものを次の(1)~(5)のうちから一つ選べ。
- ①>②>③
- ①>③>②
- ②>①>③
- ③>①>②
- ③>②>①
- 解答
(b)各平行板コンデンサへの印加電圧をそれぞれ徐々に上昇し,極板間の電界の強さが絶縁破壊電界に達したときの印加電圧(絶縁破壊電圧)の大きさの大きい順として,正しいものを次の(1)~(5)のうちから一つ選べ。
- ①>②>③
- ①>③>②
- ②>①>③
- ③>①>②
- ③>②>①
- 解答
問18
図1に示すエミッタ接地トランジスタ増幅回路について,次の(a)及び(b)の問に答えよ。
ただし,Iʙ[μA],Iᴄ[mA]はそれぞれベースとコレクタの直流電流であり,i𝚋[μA],ic[mA]はそれぞれの信号分である。
また,Vʙᴇ[V],Vᴄᴇ[V]はそれぞれベース―エミッタ間とコレクタ―エミッタ間の直流電圧であり,v𝚋e[V],vce[V]はそれぞれの信号分である。
さらに,vᵢ[V],vo[V]はそれぞれ信号の入力電圧と出力電圧,Vᴄᴄ[V]はバイアス電源の直流電圧,R₁[kΩ]とR₂[kΩ]は抵抗,C₁[F],C₂[F]はコンデンサである。
なお,R₂=1kΩであり,使用する信号周波数においてC₁,C₂のインピーダンスは無視できるほど十分小さいものとする。
(a)図2はトランジスタの出力特性である。トランジスタの動作点を[V]に選ぶとき,動作点でのベース電流Iʙの値[μA]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
- 20
- 25
- 30
- 35
- 40
- 解答
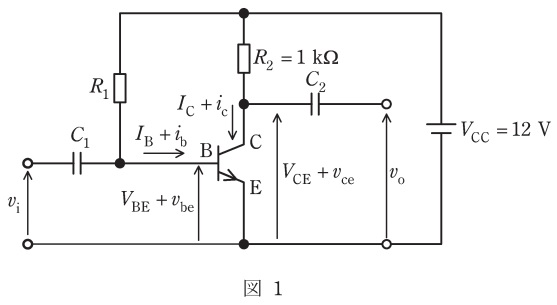
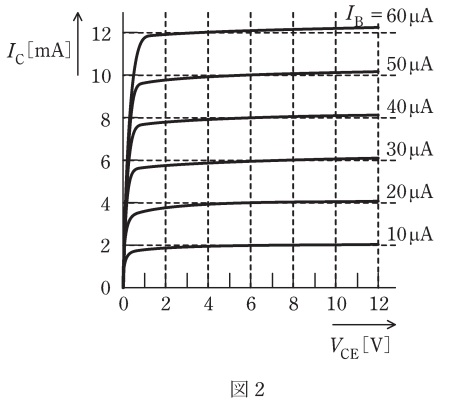
(b)小問(a)の動作点において,図1の回路に交流信号電圧vᵢを入力すると,最大値10μAの交流信号電流 i𝚋と小問(a)の直流電流 Iʙ の和がベース(B)に流れた。このとき,図2の出力特性を使って求められる出力交流信号電圧vo( =vce )の最大値[V]として,最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし,動作点付近においてトランジスタの出力特性は直線で近似でき,信号波形はひずまないものとする。
- 1.0
- 1.5
- 2.0
- 2.5
- 3.0
- 解答
正誤表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| - | - | - | - | - | - | - |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|
| - | - | - | - | - | - | - |
| 15-a | 15-b | 16-a | 16-b |
|---|---|---|---|
| - | - | - | - |
| 17-a | 17-b | 18-a | 18-b |
|---|---|---|---|
| - | - | - | - |
合計得点